Chapter 1: Introduction to Pythagorean Triples

In an unexpected twist of fate, I find myself sharing mathematical tales in English, a journey I never anticipated, especially after relocating to the UK. I aim to begin with captivating mathematical anecdotes that pique interest. Today, let's delve into some intriguing aspects of number theory.

Let's examine these two circles. Can you identify the distinction between them aside from their differing sizes?

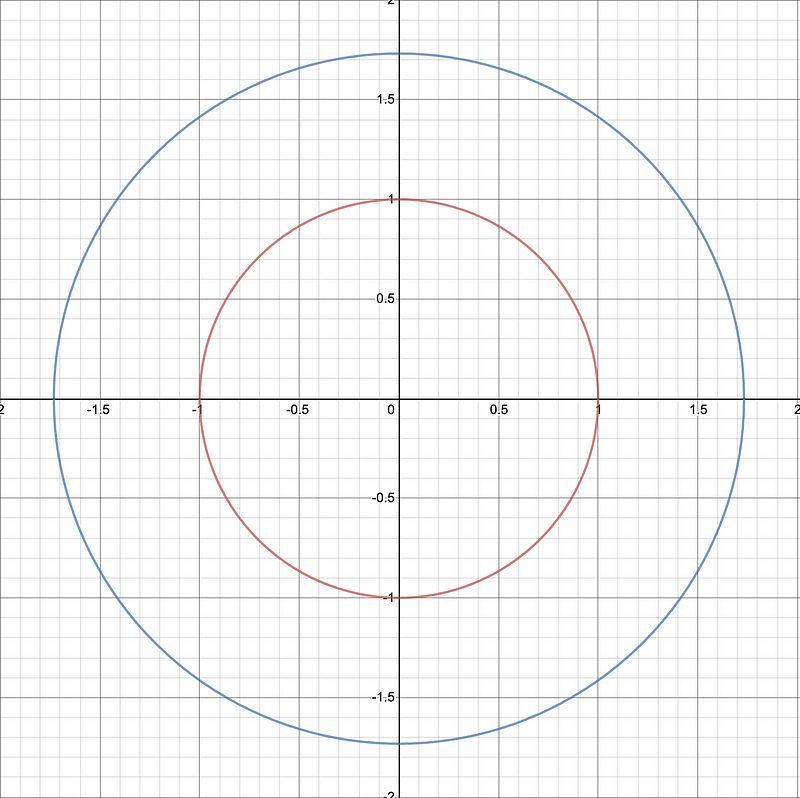
At first glance, they appear ordinary—just two circles resting on a coordinate system. However, from the perspective of Number Theory, they are as different as night and day.

Most of us likely recall the Pythagorean theorem from our school days. For a right triangle with sides (x, y, z), the relationship can be expressed as follows:

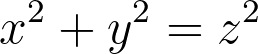
The set of numbers that fit this relationship is termed a Pythagorean triple. By dividing by z squared, we derive:

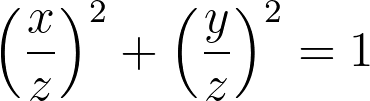
This equation can always be obtained from the previous one, provided z is not zero. The new equation not only generates Pythagorean triples but also identifies a point on a unit circle.

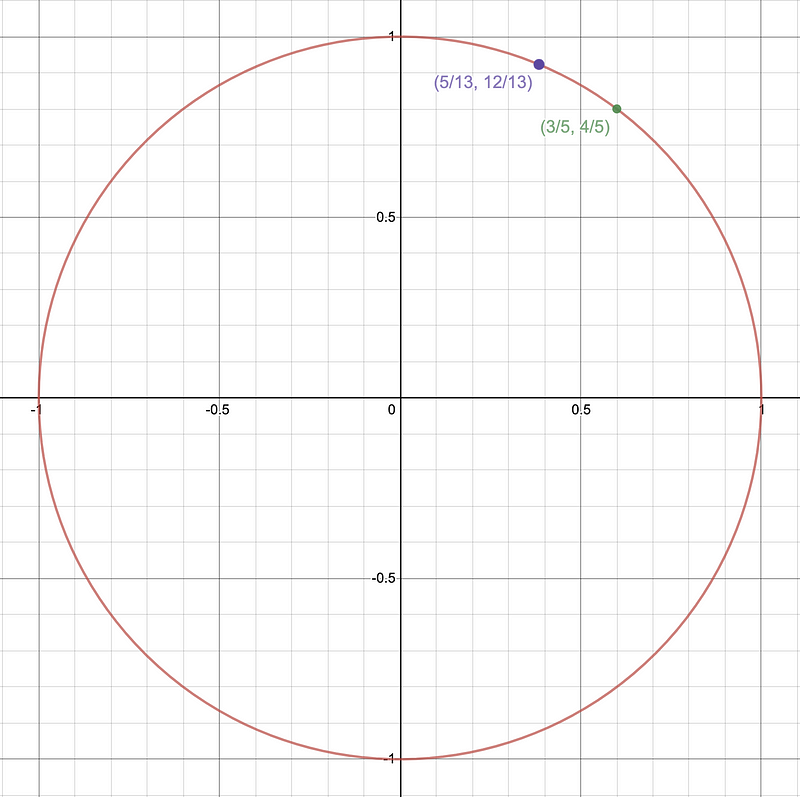
What’s fascinating is the correspondence between all Pythagorean triples and rational points on a unit circle. Recall other triples like (3,4,5) and (5,12,13)? It might take a moment to think of another, but here’s an exciting fact: there is an infinite number of Pythagorean triples! I’ll attempt to illustrate a simple proof of this.

Let's draw a line through the point (-1, 0) and another point on the circle, defined by a single parameter t.

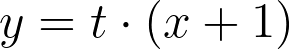
This line intersects the circle at two points, with one already known.

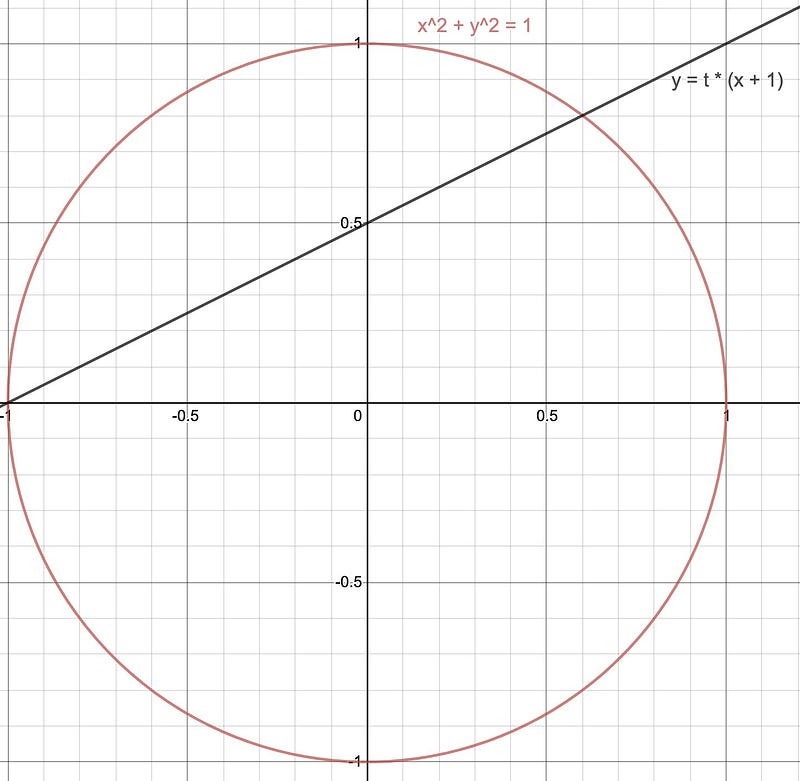
Next, we need to determine the coordinates of the second intersection point by solving these two equations simultaneously:

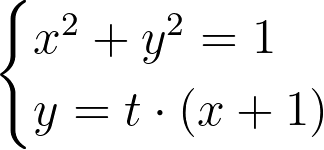
By substituting the line equation into the circle equation and simplifying, we arrive at:

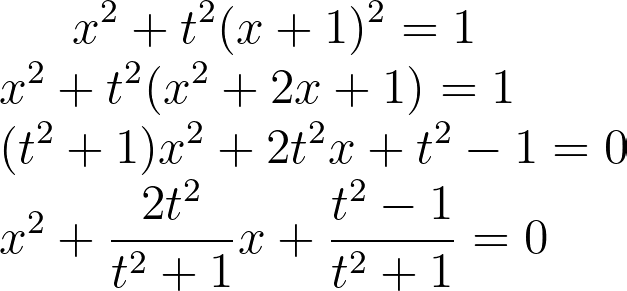
This yields a quadratic equation, which should produce two roots. We already have one, and using Vieta’s formulas, we can find the second.

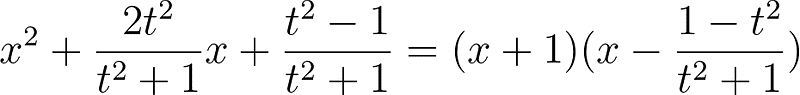
With the x-coordinate of the second point established, we can substitute this value back into the line equation to find the y-coordinate.

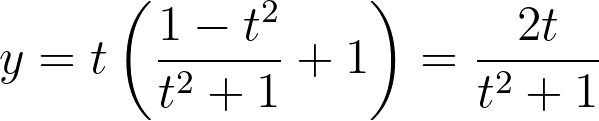
By varying the rational values of t, we can generate numerous points with rational coordinates on the circle.

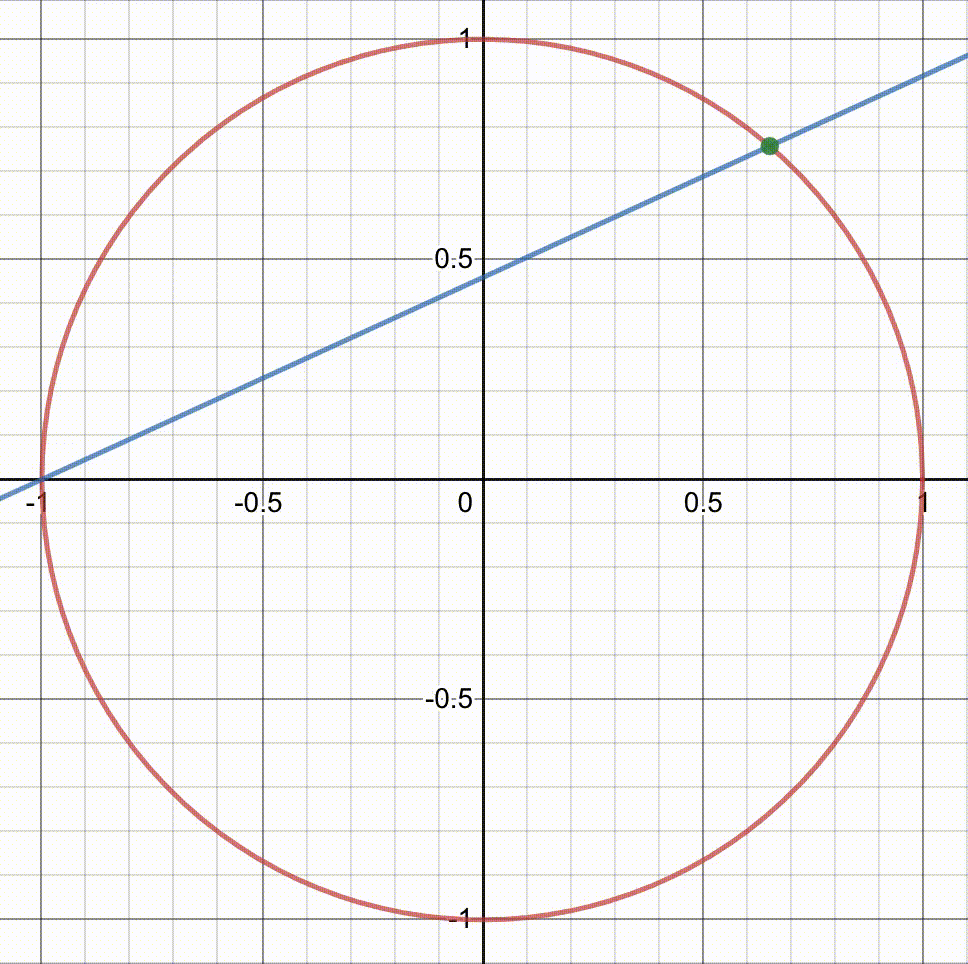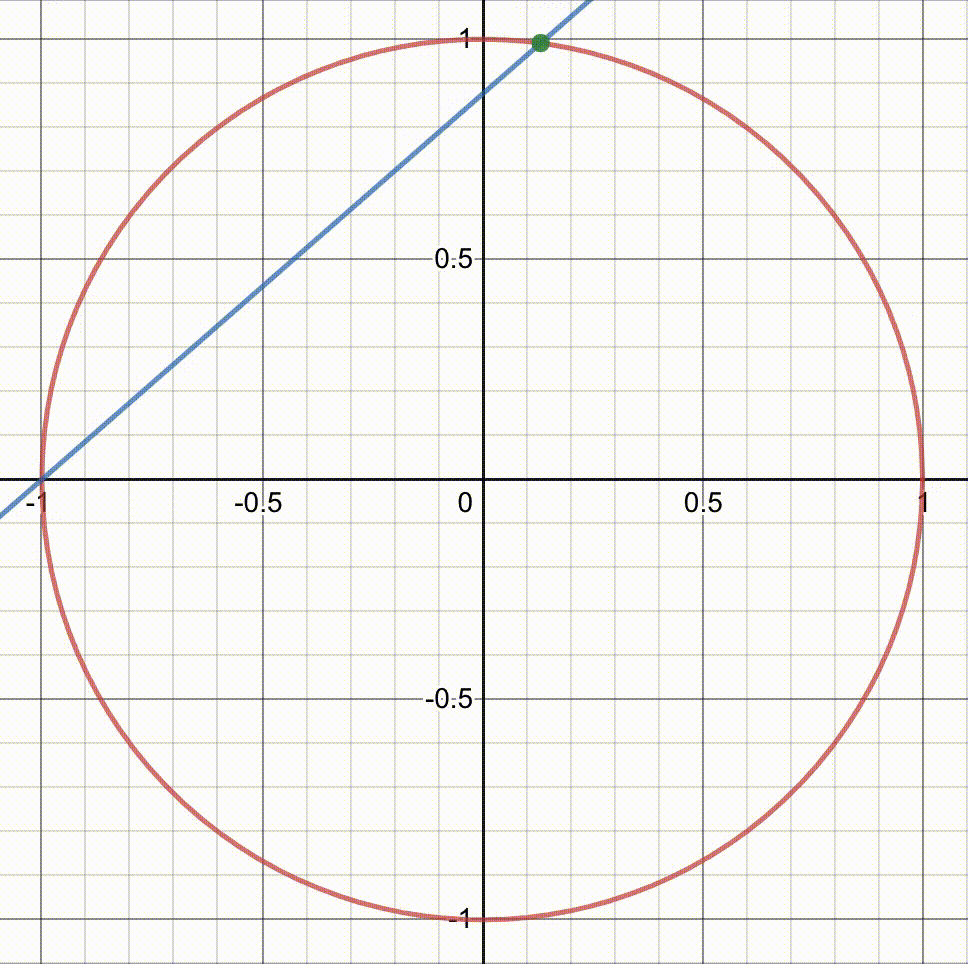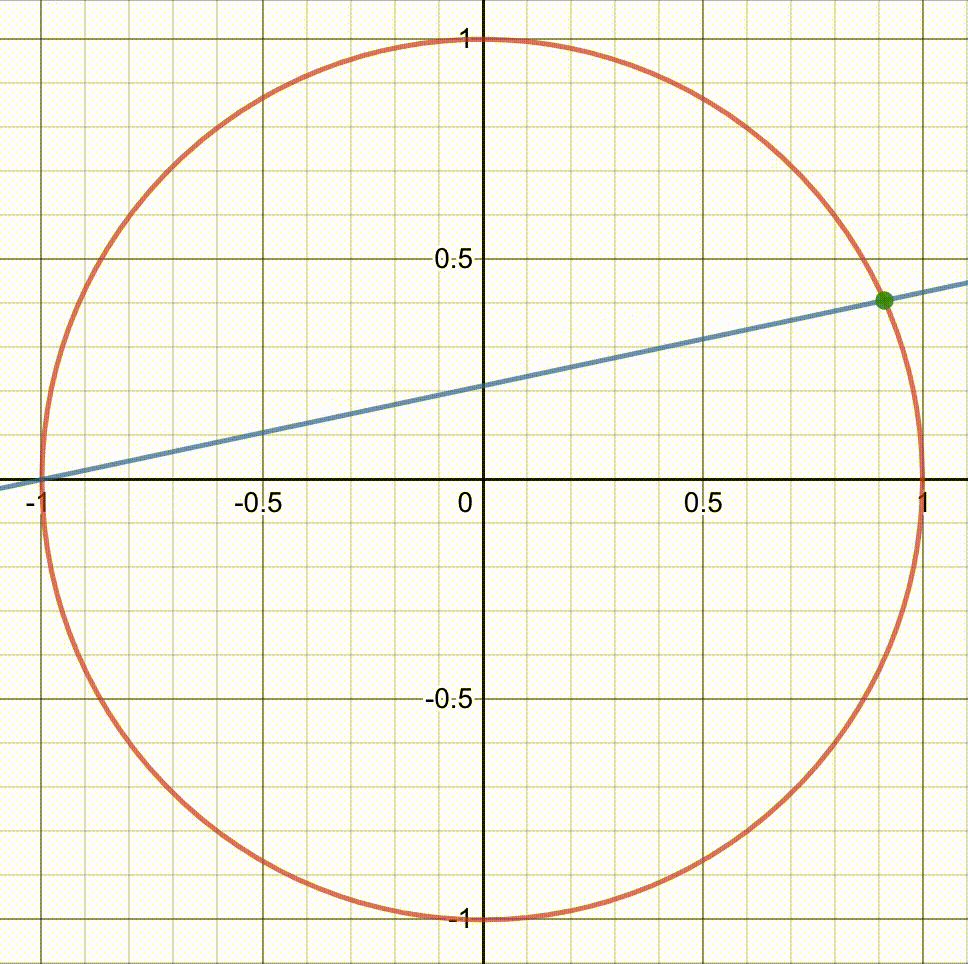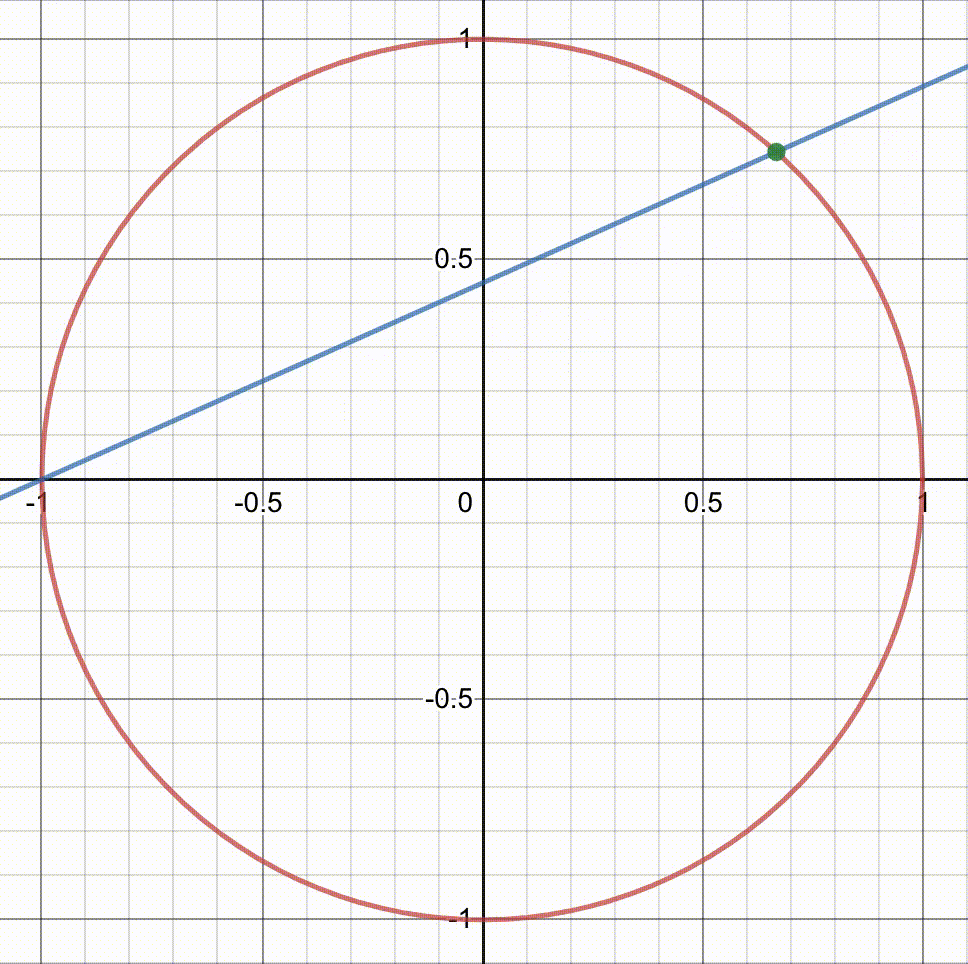
As stated earlier, each rational point on the circle corresponds to a Pythagorean triple. Can you believe it? With these straightforward steps, you can generate as many Pythagorean triples as you wish!

Now, let’s assume we know at least one rational point on a specific circle. By applying the same logic as for the unit circle, we can generate infinitely many other rational points on that circle.

So, what sets apart the two circles we discussed initially?

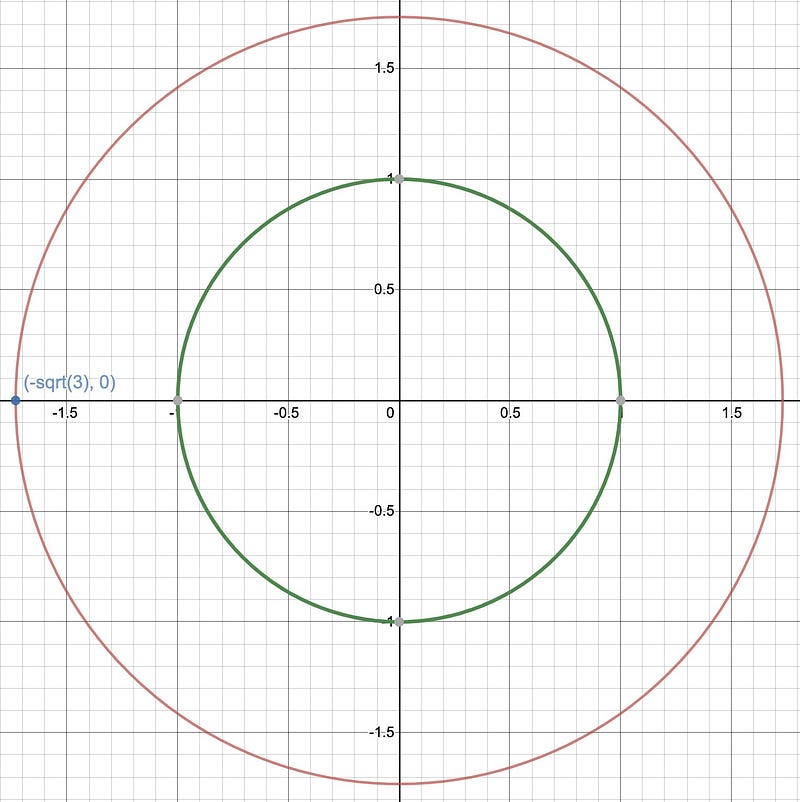
If we attempt to apply our method to the larger circle, we will encounter a challenge, as our starting point will be irrational. Consequently, all points on that circle will also be irrational. This concept is not difficult to grasp, but I will reserve the proof for future discussions.

From this, we can conclude: there are no circles that possess a finite number of rational points! This leads us to categorize all circles into two groups: those with zero rational points and those with an infinite number.

This is precisely why I find mathematics so enthralling; it allows us to derive remarkable conclusions using only basic math concepts.

Stay tuned for more mathematical explorations!

Chapter 2: Visualizing Pythagorean Triples

The first video title is "All Possible Pythagorean Triples, Visualized - YouTube," which explores the concept of Pythagorean triples through visual representations.

The second video title is "Pythagorean Triples - A Great Time-Saving Trick - YouTube," which introduces a clever method for quickly identifying Pythagorean triples.