Why Do Snowflakes Have Six Sides?

One striking feature of snowflakes is their consistent six-sided structure. While there are exceptions, it is remarkable how many snowflake types exhibit this hexagonal formation. Some display six distinct branches radiating from a central point, while others appear as six walls arranged in a hexagon. Initially, this may seem peculiar, but there is a straightforward explanation rooted in the fundamental building blocks of snowflakes: water.

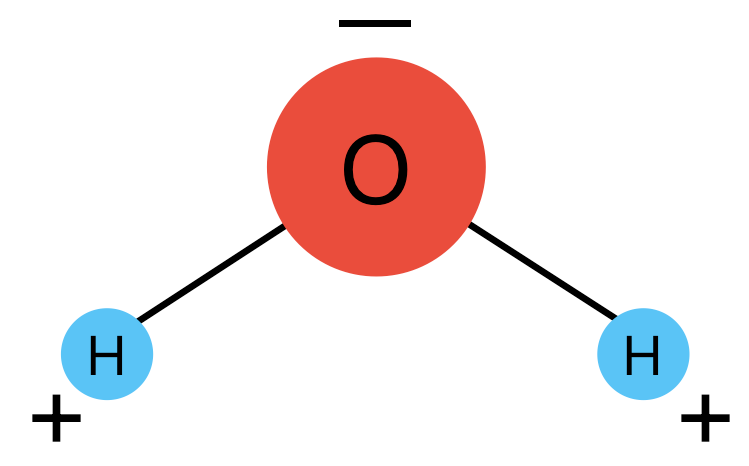
From high school chemistry, we know that water consists of one oxygen atom and two hydrogen atoms, arranged in a triangular configuration. Water is also a polar molecule, meaning it possesses a slight charge imbalance, with the oxygen atom being slightly negative and the hydrogen atoms slightly positive. This polarity leads to various unique behaviors in water, such as the tendency for spilled water to form droplets. The attraction between water molecules, due to this charge difference, plays a critical role in snowflake formation.

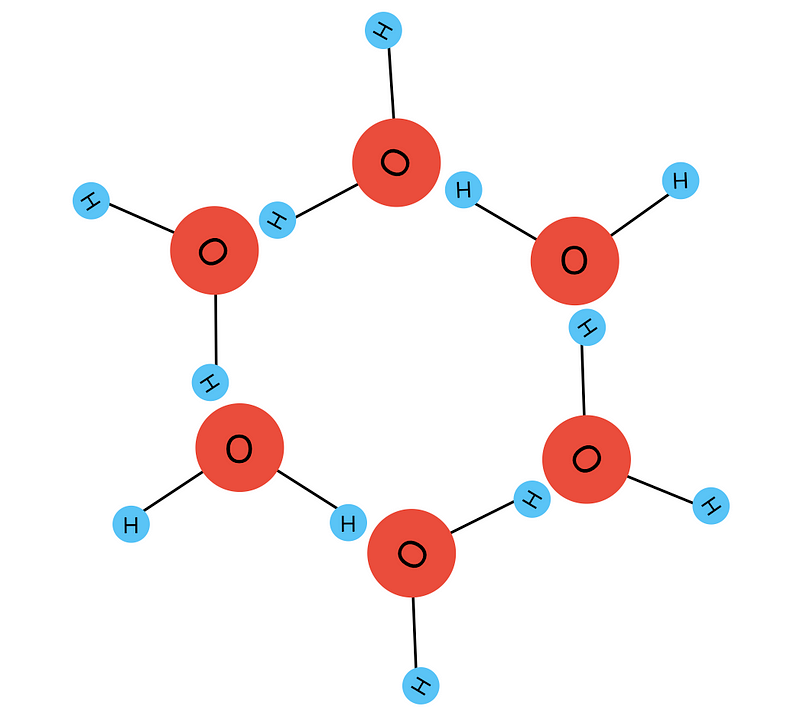
When water molecules transition into ice, they align in a way that allows the positive hydrogen atoms to gravitate toward the negative oxygen atoms. This orientation facilitates the formation of the six-sided structures characteristic of snowflakes. The spacing between water molecules is also what allows ice to float on water!

You might be curious why all six sides of a snowflake appear to grow uniformly. At first glance, this characteristic might seem puzzling, but it's actually a misconception. No snowflake is perfectly symmetrical; the ones that are photographed tend to be those that appear symmetrical to the naked eye. Upon closer inspection, however, one can find minor imperfections, even in the most beautiful snowflakes.

The Formation Process

Researchers have developed various complex algorithms to simulate the growth of snowflakes. The process begins with a nucleus, which could be a dust particle or a piece of pollen that has ascended into the atmosphere. Provided the conditions are favorable, supercooled liquid water will condense onto this nucleus, forming shapes that gradually extend outward.

This process is inherently random. Factors such as wind patterns, the path of the growing snowflake, and sunlight exposure can yield vastly different results. With so many variables at play, each snowflake is essentially unique. While it’s theoretically possible for a snowflake to be replicated, the chances are minuscule.

Here is an example of a collection of snowflakes generated through one of many simulation methods. The variety that emerges from a simple program is astonishing and closely resembles real snowflakes! Just like in nature, this process exemplifies a blend of chaos and order. A comprehensive description of the algorithm is provided at the end of this article.

Numerous methods exist for simulating snowflake creation, each with its own parameters that can be adjusted to produce different patterns. To authentically mimic snowflake growth, one would need to vary these parameters as the snowflake evolves, simulating its journey through varying temperatures and humidity levels.

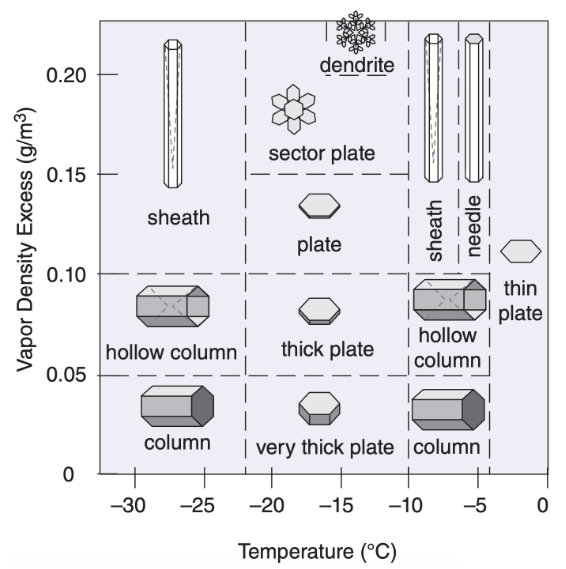
In the graph above, the x-axis represents temperature, while the y-axis indicates humidity levels in the air. Cold and warm temperatures generally produce regular ice columns. However, intricate snowflakes, known as dendrites because of their resemblance to human nerve cells, form in a specific sweet spot on the graph.

This chart serves as an idealized representation of nature, as various other processes contribute to the remarkable diversity of snowflakes.

Understanding Symmetry

While I previously mentioned that snowflakes lack perfect symmetry due to minor imperfections, they can still be conceptualized as symmetrical. This characteristic makes them suitable for analysis through a mathematical framework known as group theory. Mathematicians describe this symmetry with a group of order six, denoted as D. Although there are symmetrical groups of different sizes, snowflakes' specific structure leads to the use of the number six. If a snowflake is rotated by 60 degrees, it retains its form, with only the corners shifting. Similarly, flipping it over one of its arms yields the same result. Let’s denote a 60-degree rotation as r and a flip as f.

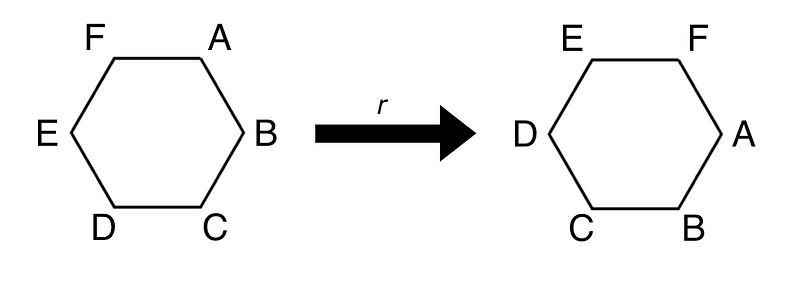
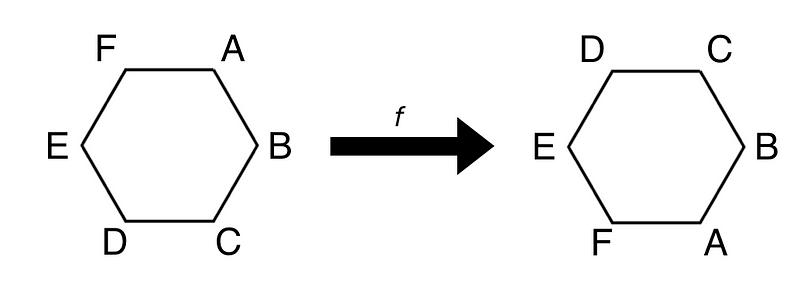
These actions can be combined. For instance, r*² indicates a 120-degree rotation, while *frf means to flip, rotate, and then flip again, with actions performed from right to left. This symmetry is unique because any combination of these two actions will result in the same snowflake. Additionally, the action e signifies that nothing happens.

To visualize this further, we can employ a Multiplication Table. Some actions can be simplified through combination, leading to an easier representation.

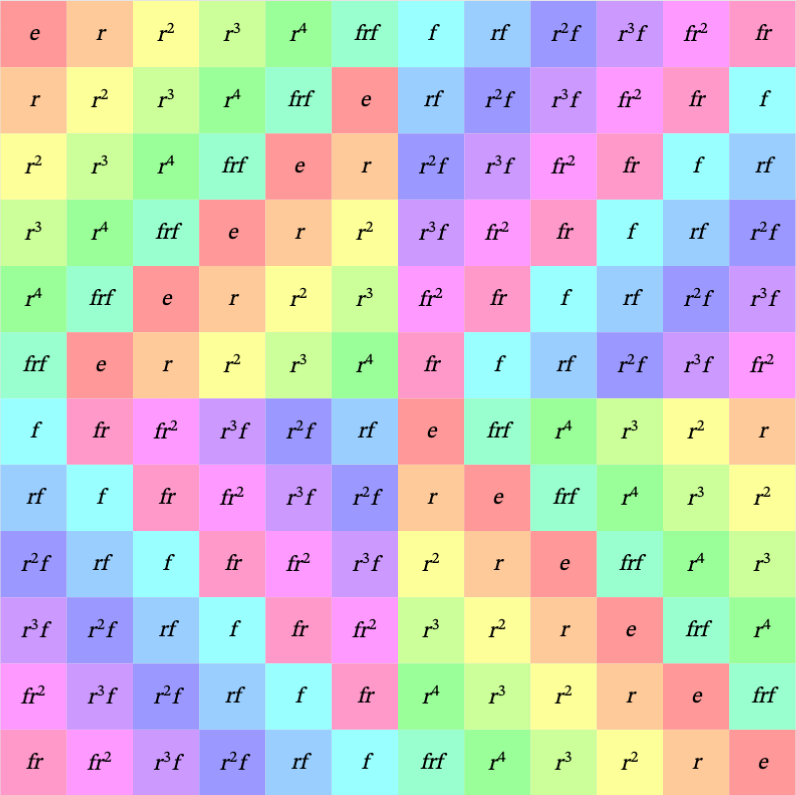
This table might seem complex at first glance, so let’s break it down. The top row lists the first set of actions, while the left side shows the second set. Each element in the table indicates the outcome of combining these actions.

Some combinations are straightforward, such as r and r yielding r*². This can be observed in the yellow square in the second position from the left and the top. Another simple combination is performing *f followed by r, which is the same as rf (remember to read actions from right to left). This result can be found seven squares to the left in the light blue square.

However, some combinations yield surprising results! Notably, r*³ is equivalent to *frf. Another unexpected outcome is that rfrf is equivalent to doing nothing, represented as e. I encourage you to test this yourself. Draw a hexagon and label its six corners, then experiment with the actions to validate the table's accuracy.

We can also visualize this group using a Cayley Diagram. Here, different color arrows represent each action, and the circles illustrate the twelve possible configurations of the snowflake's edges. For instance, e starts at the top. To execute the r action, follow the blue arrow, and then use the red arrow to perform a flip f. Notice that the flip is undirected since two flips in succession return you to the original position, while a rotation continues moving around the circle.

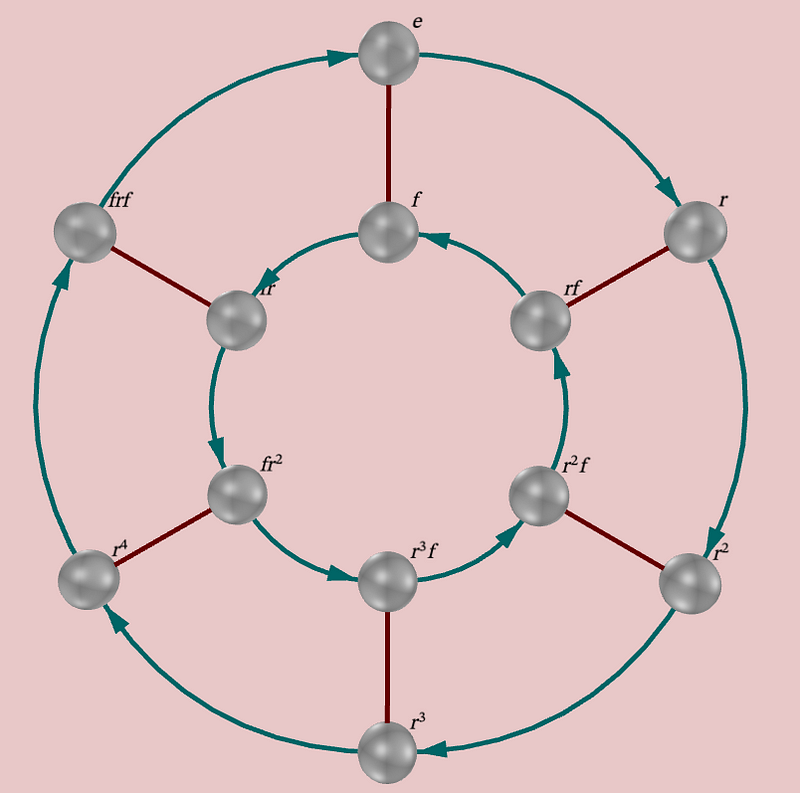
I hope this discussion helps you connect these diagrams to the symmetry found in snowflakes. In my experience, the best way to grasp group theory is through hands-on experimentation. Try different combinations of actions with a physical hexagon to see what results you obtain. Feel free to ask any questions in the comments below if you need further clarification.

Moving Forward

I hope you’ve gained some insights! Snowflakes represent a stunning aspect of nature and lead to many fascinating scientific and mathematical revelations. Their distinctive symmetry allows for analysis through advanced group theory techniques. This article only scratches the surface of the topic. If you're interested in learning more, check out the resources below!

• Looking for a textbook? Here's a free, comprehensive book titled Snow Crystals by Kenneth G. Libbrecht on arXiv, filled with valuable information.
• If you want to see more stunning snowflake images, Wilson Bentley's database of photographs is excellent. I also recommend a coffee table book with snowflake pictures.
• The YouTube channel Veritasium features a fantastic video about snowflakes, linked below.

• For those interested, the complete paper detailing the algorithm used for simulating snowflake growth is available here—it's a worthwhile read!
• If you want to explore more captivating group theory visuals, visit this page, which was referenced in this article.

Additionally, I have several related articles that you might find intriguing, so be sure to check them out!

• What is Abstract Algebra?

  Abstract algebra forms a foundational aspect of modern mathematics, encompassing a diverse range of subfields...

• The Balance of Our Atmosphere

  How do two different forces collaborate to explain wind patterns?

If you enjoyed this article, consider showing your appreciation! You might also want to follow me for more insights or subscribe to my email list for weekly updates on mathematics and science.