Understanding Time Crystals: The Impact of Perturbations
Written on
Chapter 1: Introduction to Time Crystals
In the previous discussion, we examined how a state that disrupts time-translation symmetry was achieved. The Hamiltonian presented contained a parameter labeled as h. For time-translation symmetry to be effectively disrupted, we set h to zero. This scenario is idealized; in practical situations, achieving h=0 exactly is challenging. There will invariably be experimental variations from this desired value. Therefore, it is crucial to demonstrate that time-symmetry breaking remains valid even when h is slightly perturbed.
We need to establish that a minor adjustment to h still preserves the overall integrity of the results. To do this, we analyze the energy differences between eigenstates that are locally connected. Typically, there exists an energy gap among these eigenstates. If such a gap is present, then the perturbed eigenstates will only diverge from their unperturbed counterparts through local time evolution. In this context, short-range correlated states cannot transition into long-range correlated states.
Section 1.1: Examining the Perturbation
Here, we will delve into a more rigorous analysis. We start with the unperturbed Hamiltonian, where h is set to zero. The corresponding Floquet operator is represented below.
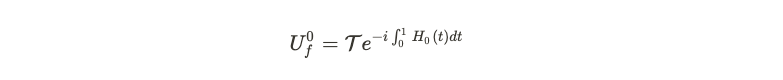
Next, we introduce a slight perturbation to h. This minor adjustment is referred to as a local perturbation, as it influences only the local aspects of the Hamiltonian—specifically, the sigma_i terms. Our goal is to demonstrate that, post-perturbation, the modified Floquet operator remains diagonal. If it retains its diagonal form, then the eigenstates will not mix (at least to the first order). This is similar to identifying an operator S that ensures the following term remains diagonal.
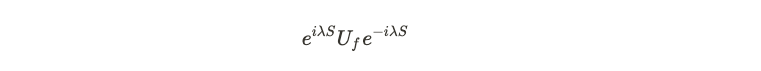
The subsequent inquiry is whether S is a local operator. If S were non-local, it could potentially link short-range correlated states with long-range correlated states. Thus, we must verify the locality of this operator. To accomplish this, we can decompose the operator into smaller components. By expressing the perturbation as a sum of these smaller elements, we can analyze the locality more effectively.
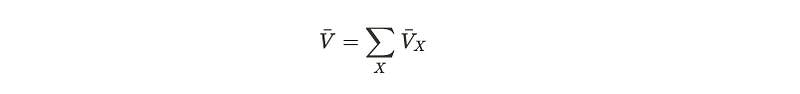
By doing so, we can also divide S into smaller segments, denoted as S_X. If we can demonstrate that these individual pieces are local, our argument will be validated.
Section 1.2: Numerical Analysis of the Floquet Operator
To ensure that numerical resonances do not compromise the symmetry breaking, we will conduct a numerical analysis of the Floquet operator, which will be discussed in a future post.
Chapter 2: Video Insights into Time Crystals
The first video titled "Quantum Time Crystals" explores the fascinating properties of time crystals and their implications for quantum mechanics.
The second video "Time Crystals: Past, Present, and Future" provides an in-depth look at the evolution of time crystals and their significance in modern physics.