Chapter 1: The Genesis of Noether's Theorem

In 1915, two mathematicians, David Hilbert and Felix Klein, approached Emmy Noether with a significant challenge. Earlier that year, Albert Einstein had introduced the field equations for his general theory of relativity, but a critical inconsistency emerged: energy conservation appeared to fail under specific conditions.

Emmy Noether, born in 1882 into a prosperous Jewish family in Bavaria, initially pursued languages before transitioning to mathematics. Her father, Max Noether, was a renowned algebraic geometry professor. Despite the restrictions on women in German universities at that time, she eventually earned her doctorate in 1907, focusing on abstract algebra and invariants—properties that remain unchanged under transformations. Her expertise in this field quickly earned her a place in the German Mathematical Society by 1909.

The two mathematicians sought Noether's unique insights in hopes of addressing the gap in Einstein's theory. Their instincts proved correct; Noether's groundbreaking work resulted in one of the most elegant outcomes in theoretical physics.

Chapter 2: Understanding Noether's Theorem

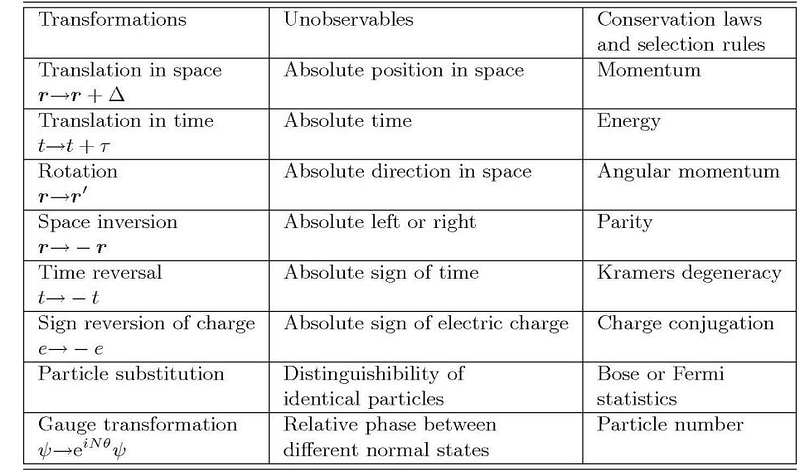
Noether's theorem can be summarized as follows: If a system's Lagrangian exhibits continuous symmetry, there exists a corresponding conserved quantity, and this relationship is reciprocal.

To clarify, a conserved quantity is a property that remains constant throughout time. For instance, the mass of a golf ball remains unchanged from the moment it is struck until it (ideally) lands in the hole, making it a conserved quantity. In contrast, the ball's velocity fluctuates due to factors like friction, meaning it is not conserved.

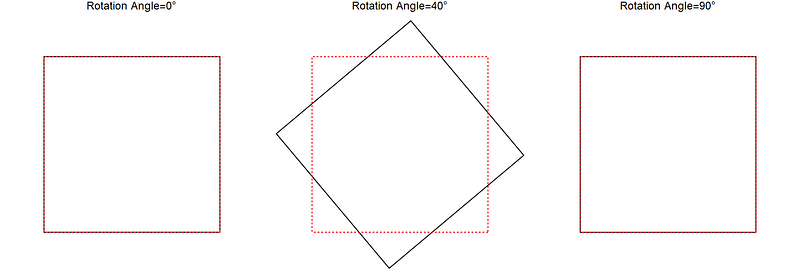
Next, consider the concept of continuous symmetry. A square, for example, has discrete rotational symmetry since it only appears unchanged when rotated by specific angles, such as 90 degrees. However, a circle possesses continuous rotational symmetry, as it looks identical regardless of the angle of rotation.

To grasp the Lagrangian, we must first understand the Principle of Least Action (PLA). This principle posits that systems evolve in a manner that minimizes the "effort" required for transitioning from one state to another. The "effort" is quantified as the action of the system.

For example, when putting a golf ball, the system transitions from "ball at my feet" to "ball in the hole." The path taken by the ball minimizes this action, illustrating PLA in action.

The Lagrangian describes how a system's energy evolves during a process to minimize action. By analyzing its behavior through differential equations known as the equations of motion, we can track how the system transitions between states.

Now, let’s return to Noether’s theorem. A Lagrangian demonstrates continuous symmetry if it remains unchanged when transformed along some coordinate. For instance, consider two identical balls colliding along the x-axis. Assuming no friction or air resistance, the dynamics depend solely on the differences in their positions and velocities, not on their absolute values. If both balls are translated by the same amount along the x-axis, their relative differences remain unchanged, implying that the system behaves consistently despite the translation. This indicates that the Lagrangian must exhibit continuous symmetry along the x-axis.

According to Noether, this symmetry corresponds to a conserved quantity—in this case, momentum. This insight forms the basis for the law of conservation of momentum. Similarly, if a Lagrangian is rotationally symmetric, angular momentum is conserved.

Chapter 3: The Implications for General Relativity

So how does this all relate back to general relativity? Hilbert and Klein had identified that energy conservation was sometimes violated within this framework. The key question was: what symmetry corresponds to energy conservation? The answer lies in time. If a system's Lagrangian does not explicitly depend on time, then energy must be conserved. Noether recognized that time translation symmetry holds only under specific conditions, particularly in flat or asymptotically flat spacetime. Consequently, energy conservation is not a universal truth in general relativity!

Through her profound understanding of abstract algebra and analytical reasoning, Noether not only addressed a critical flaw in a foundational theory of the 20th century but also illuminated a fundamental concept in theoretical physics. Her theorem underpins much of the physics we encounter in daily life, both in educational settings and beyond.

Despite her monumental contributions, Noether remains largely unrecognized. Albert Einstein himself hailed her as “the most significant, creative, mathematical genius thus far produced since the higher education of women began.” Unfortunately, she never held a permanent faculty position. Hilbert had to promote her courses under his name due to the resistance faced by female academics at that time. Following the rise of the Nazis in 1933, she emigrated to the US, where she was set to begin a position at Princeton alongside Einstein before her untimely death from cancer in 1935. One can only speculate about the discoveries that might have emerged had their talents been allowed to collaborate.

The first video, "The Most Beautiful Idea in Physics - Noether's Theorem," delves into the profound implications of Noether's Theorem on our understanding of physics.

The second video, "Noether's Theorem Explained (Part 1/6) - Introduction," provides an overview of Noether's Theorem, setting the stage for its significance in theoretical physics.

References

[4] D. Feng and G. Jin, Introduction to Condensed Matter Physics, vol. 1, Singapore: World Scientific Publishing, 2005, p. 18.

[5] D. Radford, On Emmy Noether and Her Algebraic Works, Governor’s State University, 2016.