Chapter 1: Introduction to Symbolic Calculations

The aspiration to utilize a computer algebra system as an alternative to traditional calculations has always been a goal of mine. The idea is to perform symbolic manipulations as effortlessly as scribbling on paper, avoiding the monotonous task of repeatedly writing out lengthy expressions. Although we haven't fully achieved this vision yet, advancements are being made. SymPy allows us to enhance its capabilities based on our requirements, enabling us to create a toolkit of frequently utilized functions for manual calculations. Today, I’ll be demonstrating several practical shortcuts for handling sums in SymPy.

Section 1.1: Extracting Factors from Sums

Extracting a constant factor from a sum can be surprisingly challenging in SymPy. However, we can simplify the process by creating a custom function. For example, consider the sum:

If we wish to extract the factor ( a ), our function is designed to accept both the sum and the factor to be removed:

Here’s the code for this function:

Section 1.2: Inserting Factors into Sums

This operation is essentially the reverse of factor extraction. We aim to insert a factor into a sum:

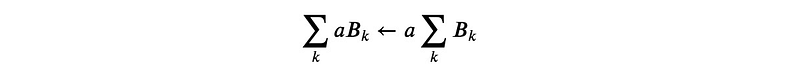
For instance:

Applying the function yields:

Chapter 2: Function Application Under the Sum Sign

The first video, "Symbolic Math with Python using SymPy - Talk Python to Me Ep.364," provides insights into using SymPy for symbolic mathematics and offers practical examples of its applications.

When dealing with the sum:

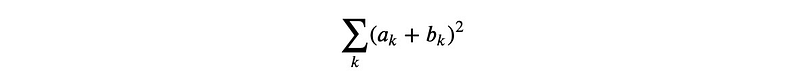
Expanding the product under the sum sign isn't achievable with SymPy's standard expand function, which produces unintended results:

The expand function not only expands but also separates the sum into multiple parts, which may not always be desirable. To maintain the integrity of the sum, it is essential to apply the expand function only to the components inside the sum. This principle applies to various functions in SymPy, including simplify and factor. Thus, it is beneficial to create a function that targets the interior of the sum exclusively.

Consider another example:

The simplify function, like expand, does not apply to the interior correctly. Our custom apply_interior function produces the desired outcome:

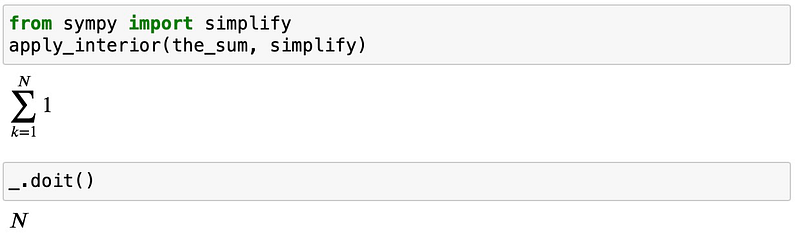
Our implementation is remarkably concise:

Chapter 3: Merging and Splitting Sums

The second video, "Symbolic Manipulation in Python," explores additional techniques for manipulating symbolic expressions, including merging and splitting sums.

In manual calculations, it is often useful to split and combine sums:

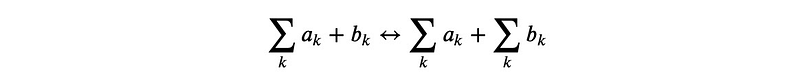
We will develop our own functions for splitting and merging sums:

And, once again, here is the code:

Conclusion

Creating custom functions for symbolic manipulation with SymPy is straightforward. While I’ve shared a few essential techniques for managing sums, I encourage you to explore further possibilities. If you have suggestions for additional applications, feel free to reach out. Thank you for your attention!