Chapter 1: Understanding Cosmic History

The vast history of our Universe is extensively understood, primarily due to our grasp of gravitational theory and knowledge of the current expansion rate and energy makeup of the cosmos. Light will perpetually traverse this expanding Universe, allowing us to receive it indefinitely into the future, though it remains constrained by time regarding what can reach us. While many questions about our cosmic origins linger, the age of the Universe is well established. The hot Big Bang event is dated to approximately 13.8 billion years ago, which aligns with our current understanding.

Determining the Universe's age may seem straightforward once you acknowledge its expansion; simply measuring the current expansion rate and applying the laws of physics helps us backtrack to the hot Big Bang conditions. This method not only works effectively but remains the most reliable way to ascertain the Universe's age. However, caution is necessary, as various simplifying assumptions can lead to misleading conclusions, as evidenced by errors made even by esteemed scientists. Here's how you can also calculate the age of the Universe.

Astronomers employ two primary techniques to gauge the expansion of space over time: standard candles and standard rulers. By observing how properties such as luminosity or angular size vary with distance, we can infer the Universe's expansion history. The candle method contributes to the distance ladder, yielding a measurement of 73 km/s/Mpc, while the ruler approach, part of the early signal method, provides a different value of 67 km/s/Mpc.

The initial step in this exploration is the Universe's expansion and the pivotal parameter we have sought to measure the longest: the Hubble constant. On a grand scale, galaxies exhibit a simple relationship between observable distance and redshift, where a galaxy's redshift corresponds to its recession speed multiplied by the Hubble constant. Remarkably, this constant is consistent across nearly all galaxies we observe, particularly those within a few billion light-years from us.

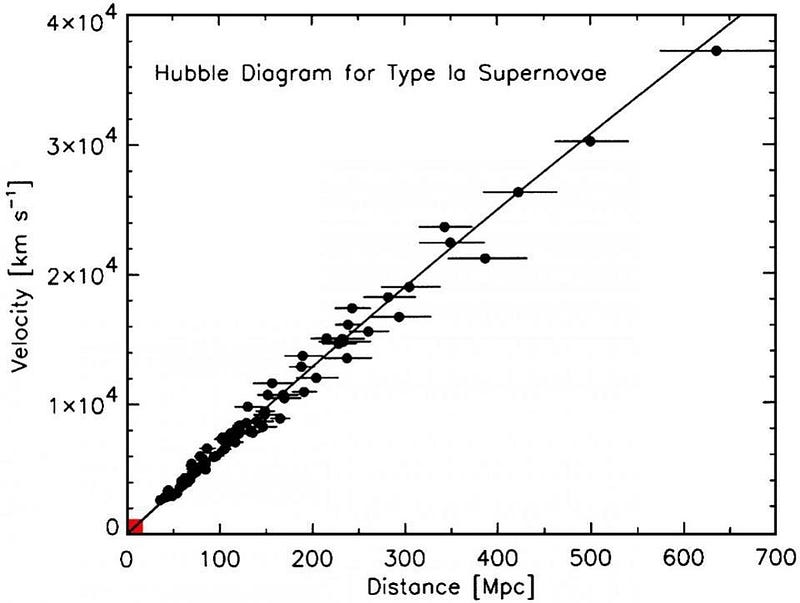
What is the Hubble constant's measured value? It varies based on how we measure it. If we use signals from the early universe, we derive a value of 67 km/s/Mpc, with a margin of error of 1–2%. In contrast, measuring light sources from a Universe that is already billions of years old yields a Hubble constant of 73 km/s/Mpc, with a 2–3% uncertainty. The discrepancy between these two values poses a significant challenge in modern cosmology.

Chapter 2: The Calculation of Cosmic Age

To comprehend how we measure the Universe's age, we must first understand the implications of the Hubble constant. This constant expresses a speed (km/s) relative to distance (Mpc), meaning that a galaxy located 100 Mpc away should recede ten times faster than one only 10 Mpc distant, and only one-tenth as fast as a galaxy 1,000 Mpc away. This illustrates the fundamental redshift-distance relationship.

Interestingly, we can also interpret the Hubble constant as an inverse time, suggesting a potential correlation with the Universe's age. For instance, if the Hubble constant is 67 km/s/Mpc, it corresponds to an age of 14.6 billion years, whereas a value of 73 km/s/Mpc equates to an age of 13.4 billion years. Both estimates align closely with the accepted age of the Universe but differ by approximately 9%.

However, adjusting the Hubble constant does not directly alter the Universe's age due to crucial underlying factors.

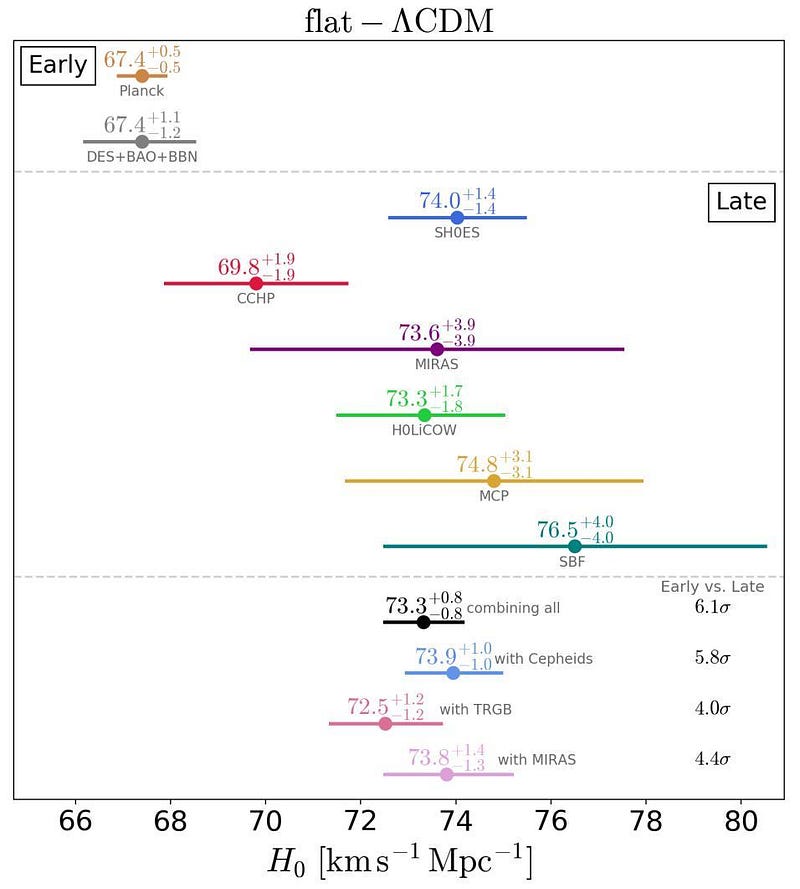
The present value of the Hubble constant is not merely the inverse of the Universe's age despite the mathematical relationship. Instead, this expansion rate must balance the total energy contributing to the Universe's makeup, encompassing normal matter, dark matter, neutrinos, radiation, dark energy, and spatial curvature, among other factors.

The equation governing the Universe's expansion, derived by Friedmann in 1922, illustrates the relationship between these variables.

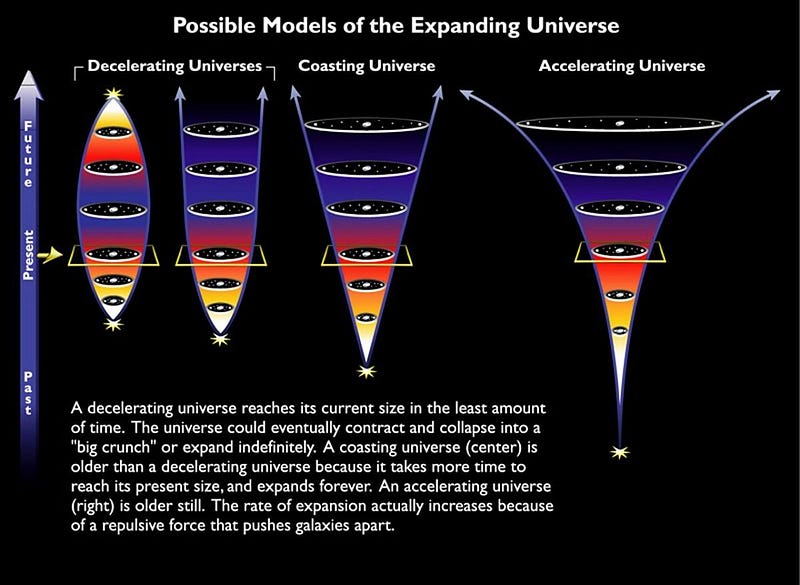
In a Universe composed solely of radiation, the product of the Hubble constant and the Universe's age equals ½. In a matter-dominated Universe, that product equals ⅓. Conversely, if a Universe comprises only dark energy, the product continually increases over time, illustrating that knowing the Universe's composition is essential for accurately calculating its age.

To ascertain the Universe's age since the hot Big Bang, we must determine both its expansion rate and its composition. Various methods exist for this, but crucially, our measurements of one parameter often hinge on our assumptions about the Universe's makeup. For example, the Cosmic Microwave Background (CMB) radiation provides vital insights into the early Universe's characteristics.

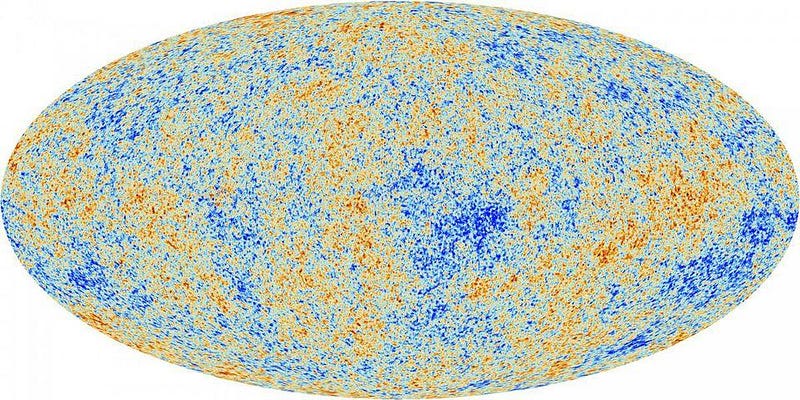
The CMB represents the residual radiation from the Big Bang, displaying slight irregularities and temperature variations on a scale of mere hundredths of a degree. Although these fluctuations play a significant role at later times, their impact on the early Universe's large-scale structure is minimal. The Planck satellite has captured these fluctuations with unprecedented accuracy, enabling us to derive constraints on the Universe's expansion rate and composition.

Through these fluctuations, we can discern critical details about the Universe's makeup, such as the proportions of normal matter, dark matter, and dark energy, which all lead to the same conclusion regarding the Universe's age.

In conclusion, while there are various combinations of values that can fit the observed data regarding the Universe's composition and expansion speed, they consistently indicate that the Universe is approximately 13.8 billion years old. This precision arises from the comprehensive data available, ensuring that regardless of the specific makeup of the Universe, its age remains a well-established fact. To accurately assess the Universe's age, one must consider its composition to avoid naive and incorrect conclusions.