Unlocking the Secrets of Cambridge: A Calculus Challenge
Written on
Chapter 1: Introduction to the Challenge
Can you gain admission to Cambridge University? This calculus puzzle is designed for prospective computer science students eager to demonstrate their analytical prowess. The question may seem simple at first glance, but dig deeper—there's more than meets the eye. Here’s a tip: try substituting some values to find your way through!
Before moving on to the solution, take a moment to pause, grab your pen and paper, and give it a shot. When you’re ready, continue reading for the answer!
Solution Overview
All given functions are definite integrals with limits from 0 to 1. Therefore, our focus should be on examining how these functions behave within this interval. Notably, each function is increasing since their derivatives are positive.
To better understand the relationships among these functions, we’ll evaluate them at three distinct points: x = 0, x = 1/2, and x = 1.
Evaluating at x = 0
At x = 0, it's clear that all functions yield a value of 1, as any real number raised to the power of zero equals one.
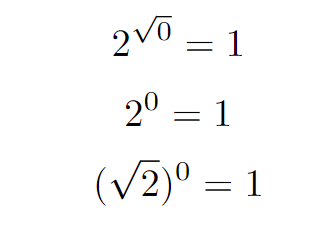
Evaluating at x = 1/2
This is where things get a bit trickier. Let's focus on the first function.
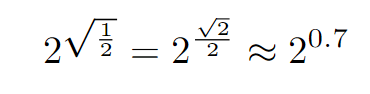
Notably, the square root of 1/2 can be simplified to √2 / 2, which approximates to around 0.7. This is crucial because for values between 0 and 1, the square root exceeds the original number, confirming that 0.7 is greater than 0.5.
The second function is simpler, as it is merely the square root of 2, which is indeed less than the previous function.
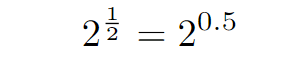
For the third function, we apply index laws.
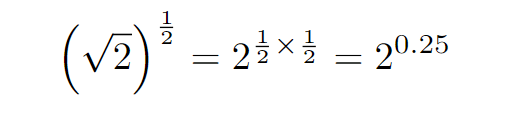
We find that this function yields the lowest value among the three. So far, our order of the functions appears to be R < Q < P.
Confirming with x = 1
Next, we evaluate at x = 1.
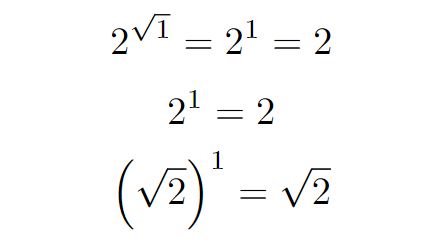
Here, integrals P and Q equal the same value, while integral R remains lesser than the other two.
With all this information, can you visualize what the graphs of these functions might look like?
![Graphs of the three functions on the interval [0, 1]](https://4008063323.net/all_images/2024-09-25/67433_7.jpg)
Indeed, all three functions are increasing within the interval. The colors representing them are as follows: P is blue, Q is red, and R is green.
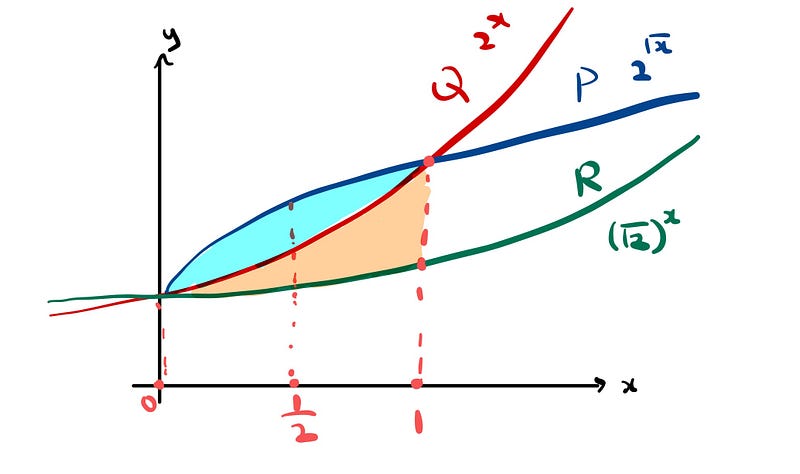
The blue shaded area indicates that P surpasses Q, while the orange region shows that Q is greater than R.
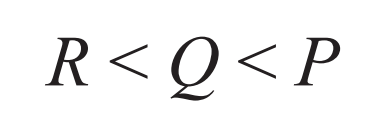

Did you know that the famous mathematical bridge is located at Cambridge University? How fascinating!
What were your thoughts while solving this problem? I would love to hear your insights in the comments below!
Math Puzzles to Explore
Engage with a variety of mathematical puzzles, including Algebra, Geometry, Calculus, Number Theory, and more. Share these with your friends and family!
Discover the journey of an international student getting into Cambridge University through this insightful video.
Watch students share their thoughts on how to gain admission to Cambridge University in this street interview.
Thank you for reading! If you found this article informative, please show your support by clapping. Your encouragement motivates me to continue writing.
If you're interested in tailored math puzzles, feel free to reach out!
Love, Bella