Chapter 1: The Intriguing Question of Photon Speeds

What happens to the relative speed when two photons are traveling directly towards one another? This frequently posed question often substitutes starships for photons, which complicates matters since a massive object cannot attain light speed.

At first glance, it may seem logical to simply add the speeds of the two photons. However, this approach is misleading. According to relativity, time is experienced differently by observers in varying frames of reference. While this notion may initially appear counterintuitive or illogical based on our daily experiences, it primarily stems from the fact that we do not encounter speeds approaching that of light in our everyday lives.

The phenomenon of time dilation, resulting from near-light speed travel, can be effectively calculated using Lorentz transformations. For instance, the Lorentz factor, which serves as a proportionality constant for time, is derived using the following formula:

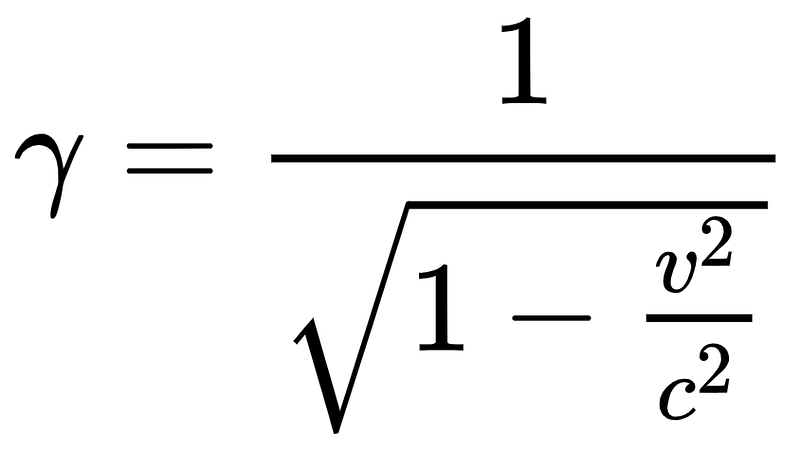
As an object's speed escalates, the effects of time dilation become pronounced: in its own frame of reference, time begins to pass more slowly. This is not mere speculation; it has been confirmed through experiments. For example, when synchronized atomic clocks are sent into orbit at significant speeds, they experience desynchronization, precisely as predicted by relativity. Notably, clocks aboard the International Space Station (ISS) lag behind those on Earth by 0.01 seconds annually.

Despite the minimal nature of this effect, it can be accurately measured with high-precision instruments and is crucial in the design of space technology.

Now, returning to our photons: what is the relative speed at which two photons approach each other? From an external observer's viewpoint, the separation between the two photons appears to decrease at twice the speed of light. This might seem to contradict the principles of relativity, yet it does not.

In this context, the doubled speed of light does not represent the velocity of a tangible object within the observer’s frame of reference; rather, it reflects the rate at which the distance between the two photons changes. Importantly, a change in distance does not constitute a physical object. Each photon maintains its speed at light speed in the observer's frame.

But what if we tried to associate an inertial frame of reference with one of the photons? Unfortunately, this is unfeasible, as no frame of reference can exist where a photon is stationary. If we attempt to insert light speed into the Lorentz factor equation, it results in division by zero, rendering the expression nonsensical.

However, we can consider electrons or spacecraft traveling at 0.9 times the speed of light instead of photons. For these sublight speeds, we can easily define a frame of reference. In the frame of one of the vessels, time does not progress uniformly as it does in the other ship's frame, and the standard method of simply adding velocities does not apply. Instead, using Lorentz transformations, we derive the relativistic formula for combining speeds:

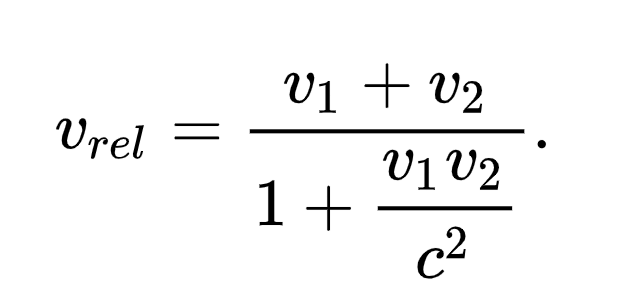
By substituting 0.9 times the speed of light for both v1 and v2, we can compute the relative speed of the two ships, resulting in 0.9945 times the speed of light—significantly close to light speed, yet still below it.

Clap if you want to see more articles about space in your feed!

Subscribe to our channel and share your questions, which I will address in future articles.

If you appreciate my content, consider supporting me by becoming a Medium member for just $5 monthly, helping us create even better material.

Chapter 2: Exploring Relativistic Speeds

In this video titled "Relative velocities of objects moving with nearly the speed of light," the nuances of relativistic speeds are explored in depth, providing a clearer understanding of how speeds are perceived differently based on relative motion.

The video "Relativistic Velocity at Speed of Light" delves into the complexities of how speeds approach light speed, further illustrating the principles discussed in this article.