Understanding Nested Radicals: Exploring Integer Parts in Math
Written on
Chapter 1: The Concept of Nested Radicals
In nature, mother birds carefully create nests using various materials to keep their eggs safe and warm. Similarly, in mathematics, we can nest radicals within one another as many times as needed. Today, we will tackle a problem involving a nested radical expression.
Before we proceed, consider using a strategic substitution to simplify the problem. Take a moment to work through it with pen and paper, and then continue reading for the solution!
Solution
To start, we recognize that 72 exceeds the square of 64.
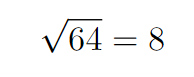
This indicates that A, the integer part of our expression, must be at least 8.
Upper Bound Construction
Let’s explore an upper bound by substituting the innermost 72 with 81.
The interesting twist is that since the square root of 81 equals 9, we can streamline the expression as shown below.
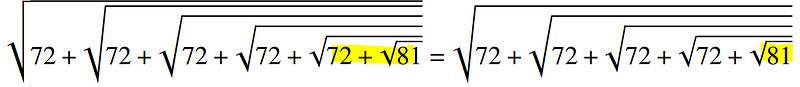
Notice how we can rewrite 72 + (the square root of 81) as 72 + 9 = 81, which is then placed under another square root! This process continues until we reach 9.
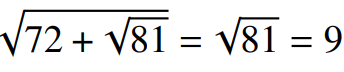
This final expression is slightly larger than what we initially sought, allowing us to determine a range for the integer A.
Conclusion
Consequently, A must equal 8!

And there you have it! What were your thoughts during this process? Feel free to share in the comments—I'm eager to hear your insights!
The first video explores how to find the integer part of a radical expression, breaking down the concept in an engaging manner.
In the second video, the basics of integer parts are discussed, offering a clear overview of this mathematical concept.
Math Puzzles
Discover a collection of intriguing math puzzles that span various topics including Algebra, Geometry, and Calculus. Share these with your friends!
Thank you for reading! If you found this article helpful, don't forget to show your appreciation.

Support my work if you can! Your generosity means a lot and helps me continue creating valuable content. Happy solving!