Chapter 1: The Concept of Infinity

Infinity represents an idea of boundlessness, a notion that has intrigued philosophers since the days of ancient Greece. This concept became a significant topic of philosophical inquiry, eventually evolving into a subfield of philosophy itself. By the 17th century, the study of infinity intersected with calculus, particularly through the exploration of infinitesimals (infinitely small values), often represented as 1/?. Surprisingly, the concept of infinity finds practical applications in various real-world contexts, ranging from autonomous vehicles to the maintenance of water tanks.

It's easy to become entangled in the notion of infinity, particularly when we treat it as a number. In line with its philosophical implications—representing the greatest possible number—it might seem logical to assert that:

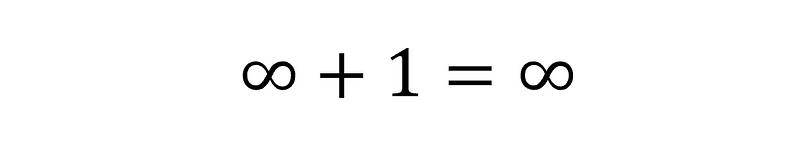
However, this leads to contradictions when we attempt to apply infinity alongside other numbers, such as the claim that 1 equals 0. Consequently, such mathematical assertions are often dismissed as nonsensical. Even if we discard the more rigorous interpretation that infinity plus one still equals infinity, the philosophical understanding of infinity suggests that it makes sense as a concept. Rather than being a fixed number, infinity can be viewed as an ongoing process, akin to continuously adding one to the largest known number. While humans find it convenient to conceptualize this abstract idea as a numerical value, it's essential to recognize that in calculus, infinity is treated not as a number but as a concept, distinct from finite numbers and their properties.

The idea that there exist infinities of different sizes may come as a surprise, especially considering our limited understanding of infinity. Cantor's famous diagonal argument illustrates that infinite sets can indeed differ in size. For example, consider the infinite set of all integers (1, 2, 3, …) versus the infinite set of real numbers (0.5, √2, π, among others). Instinctively, we sense that there are more real numbers than integers. Can we even compare the lengths of these sets?

Cantor's diagonal argument posits that an infinite set T and the infinite set of natural numbers (positive integers: 1, 2, 3, …) are not the same size.

The first video explains the sizes of infinite sets and provides visual insights into Cantor's argument.

Consider set T as consisting of various subsets of infinite sets, denoted s?, each containing 0s and 1s. Since there are infinitely many such sets s?, the set T is also infinite.

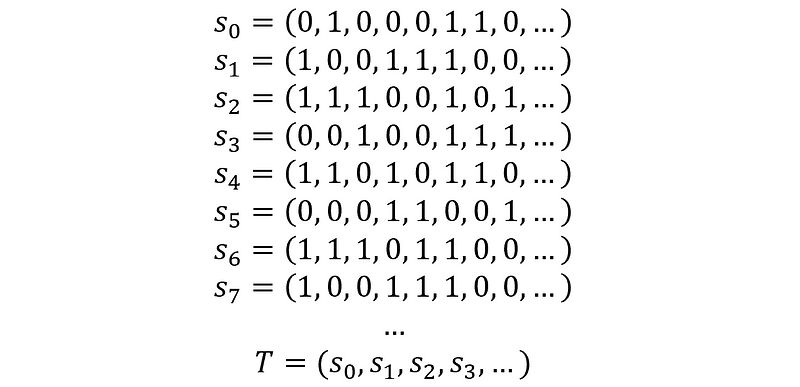
Moreover, set T can be put into a one-to-one correspondence with the set of natural numbers N, indicating that T and N are equivalent in size.

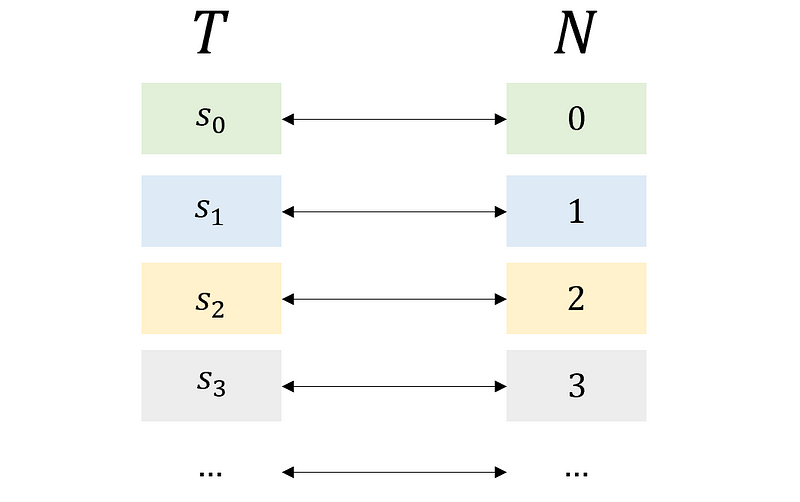
To illustrate this, construct a sequence q where, for each index n starting from 0 and continuing to infinity, the nth index of q is the opposite of the nth index of the nth element of T (T[n]). This forms the diagonal in Cantor's argument.

The set q cannot match any of the elements in T, as their nth digits will always differ. Thus, by its very construction, q is distinct from any member of T, even though T encompasses every conceivable infinite combination of 0s and 1s.

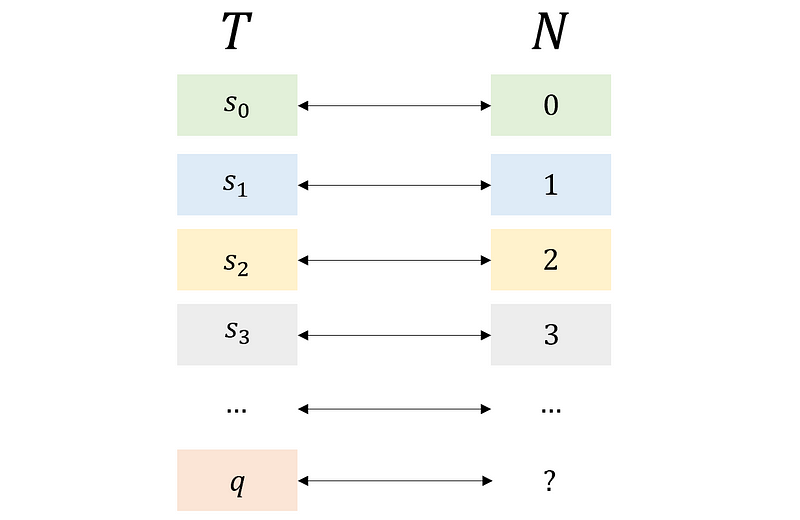
In addition, we can create a new sequence m that remains unique from all elements in T, including q. Consequently, even though set T is infinite, it continually expands with new, unique elements. In this regard, T can be regarded as infinitely larger than the set N, despite both being infinite sets.

Cantor's diagonal argument reveals that there are multiple infinite sets of differing sizes. Whether it clarifies our understanding or adds complexity, the nature of infinity remains a captivating subject!

Chapter 2: Exploring Different Sizes of Infinity

The second video delves into set theory and the various sizes of infinity, providing deeper insights into this intriguing mathematical concept.