Chapter 1: Introduction to Polyhedra

Euler's Formula is a renowned concept in mathematics, often referred to by the name of its creator, Leonhard Euler (pronounced "Oy-luh"). A polyhedron is defined as a three-dimensional shape with flat polygonal faces, where each side of a face aligns precisely with another face.

To illustrate this, consider the Dodecahedron, which consists of twelve pentagonal faces.

Next, let's examine a few more polyhedra: the Cube, the Tetrahedron, and another shape that features both square and triangular faces.

By noting the counts of vertices (V), edges (E), and faces (F) for these four shapes, we can observe an interesting pattern:

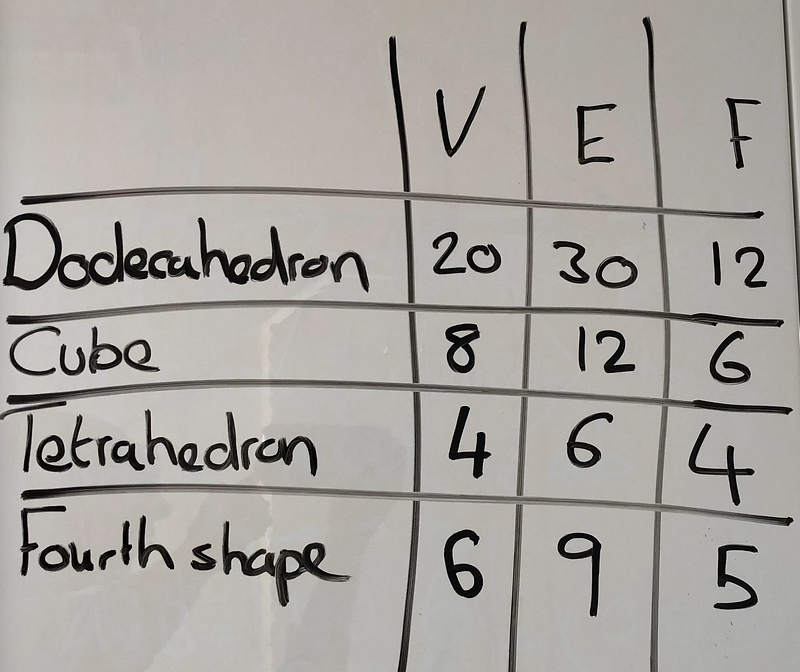
The equation V - E + F = 2 appears to be consistently valid. This remarkable relationship holds true for all convex polyhedra. We can express this theorem formally as follows:

Theorem A: For any convex polyhedron with V vertices, E edges, and F faces, the equation V - E + F = 2 is always satisfied.

In this context, "convex" means that a straight line drawn between any two vertices will remain entirely within the polyhedron. While the examples given are all convex polyhedra, consider a scenario where a smaller cube is removed from the center of a larger cube. This modified shape has 16 vertices, 24 edges, and 12 faces, leading to V - E + F = 4, which deviates from the expected 2.

To establish the validity of this theorem, we will approach the proof through two-dimensional representations rather than three-dimensional ones. The logic is accessible to most individuals.

Chapter 2: Proving Euler’s Formula

To begin proving this theorem, we first need to define a key term and present another theorem that will assist in our demonstration.

Definition: A plane graph is a two-dimensional figure composed of vertices and edges connecting these vertices, ensuring that no edges intersect. A plane graph is deemed connected if it is possible to travel from any vertex to another by following a path along the edges.

Here are some examples of connected plane graphs:

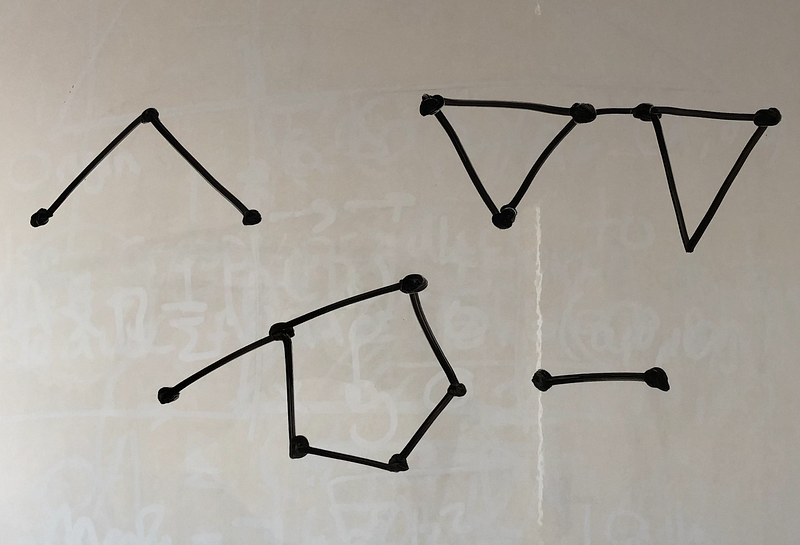
It appears that for these graphs, V - E + F = 1 holds true. We will demonstrate below (Theorem B) that this formula is valid for all connected graphs.

This finding is instrumental in proving Theorem A, as we can closely observe one face of the Cube, Tetrahedron, or the mixed-face shape and represent it on paper, yielding a connected graph like this:

Therefore, we can conclude that all convex polyhedra can be interpreted as connected plane graphs (considering one face removed). Thus, if V - E + F = 1 for all connected plane graphs, it follows that V - E + F = 2 for all convex polyhedra.

Theorem B: For a connected plane graph with V vertices, E edges, and F faces, it holds that V - E + F = 1.

Proof: Begin by examining plane graphs with a single edge; there exists only one such graph that clearly consists of 2 vertices, 1 edge connecting them, and 0 faces. The formula holds true since 2 - 1 + 0 = 1.

However, we wish to extend this to any connected plane graph with any number of edges. We can utilize a method known as Mathematical Induction, which asserts that if a statement P(k) is valid for some integer k, and we can demonstrate that P(k+1) is also valid, then this must imply that P(n) is true for all integers n greater than k.

Consider our statement P(k) defined as V - k + F = 1 for all connected plane graphs with k edges. Notably, P(1) is certainly true (as shown previously). Assuming P(k) is true, we seek to prove P(k+1).

For P(k+1), any connected plane graph with k+1 edges will necessarily have at least one face or lack one. If it contains at least one face, we can remove an edge from that face. The resulting connected plane graph will retain V vertices, have F - 1 faces, and k edges. We can then apply the assumption that P(k) is valid, yielding V - k + (F - 1) = 1, which can be rearranged to V - (k + 1) + F = 1, confirming the validity of P(k+1) for graphs with at least one face.

Conversely, if the graph does not contain a face, it must have an end vertex—one that connects to an edge on one side but not the other. By removing this end vertex and its corresponding edge, we obtain a new connected plane graph with V - 1 vertices, k edges, and 0 faces. Again, applying P(k) leads us to (V - 1) - k + 0 = 1, which rearranges to V - (k + 1) + 0 = 1, affirming the validity of P(k+1) for graphs without faces.

Thus, Theorem B is established, confirming that Theorem A holds true.

In conclusion, it is commonplace for mathematicians to approach problems from various angles to simplify proofs. In this case, we reinterpreted the challenge involving convex polyhedra as a question about connected plane graphs. For those interested in practical applications of this theorem, refer to my other piece titled "Known since Antiquity: The Platonic Solids."

The first video titled "Euler's Formula for Polyhedra | Math with Mr. J" provides an engaging overview of Euler's formula and its significance in geometry.

The second video, "How to use Euler's Formula for Convex Polyhedra to Find the Number of Vertices Given Faces and Edges," offers practical insights into applying Euler's formula to various shapes.