# Understanding Computational Complexity: A Comprehensive Overview
Written on
Chapter 1: Introduction to Computational Complexity
In the realms of computer science and software engineering, the concepts of "algorithmic complexity" and "computational complexity" are integral. These terms describe the amount of time or memory required to execute a specific task or a series of tasks. Essentially, they provide insight into the efficiency of an algorithm and the necessary hardware resources for task execution. Computational complexity is generally categorized into two types: time complexity and space complexity. This article will delve into how to assess the computational complexity of various algorithms, with illustrative examples in Python.
To measure complexity, we utilize a notation known as Big-O. For instance, if an algorithm needs a total of 2n + 1 computations to complete, where n signifies the number of computations, we can express its complexity as O(n). This is termed "linear" complexity, as the dominant term is n raised to the first power. Consequently, constant factors like 2 and 1 can be disregarded since the algorithm's complexity scales linearly with n; that is, doubling n will also double the total execution cost.
There are various classifications for complexity. For example, an algorithm is said to have constant complexity denoted as O(c) or O(1), indicating that its cost remains unchanged regardless of the size of n. However, such cases are rare and typically pertain to specialized scenarios, such as determining whether a number is odd or even. Another notable complexity is O(log(n)), which is advantageous because it increases very slowly even as n grows large, resembling constant complexity closely. Generally, the complexity is defined by its “largest growing term.” For instance, consider the function:
f(n) = 3n² + 2n + 10
Here, the term n² dominates as n becomes very large, leading us to classify its complexity as quadratic, or O(n²). In this scenario, increasing operations tenfold results in a hundredfold increase in running costs, which is significant. Typically, Big-O notation is categorized according to polynomial degrees or combinations of polynomials with logarithmic functions, such as O(n log(n)), which is more efficient than O(n²). As polynomial degrees rise, we encounter worse complexities, such as exponential O(2^n). In computer science, O(n!) (factorial complexity) is considered the least efficient, as it escalates so quickly that it could potentially crash your system.
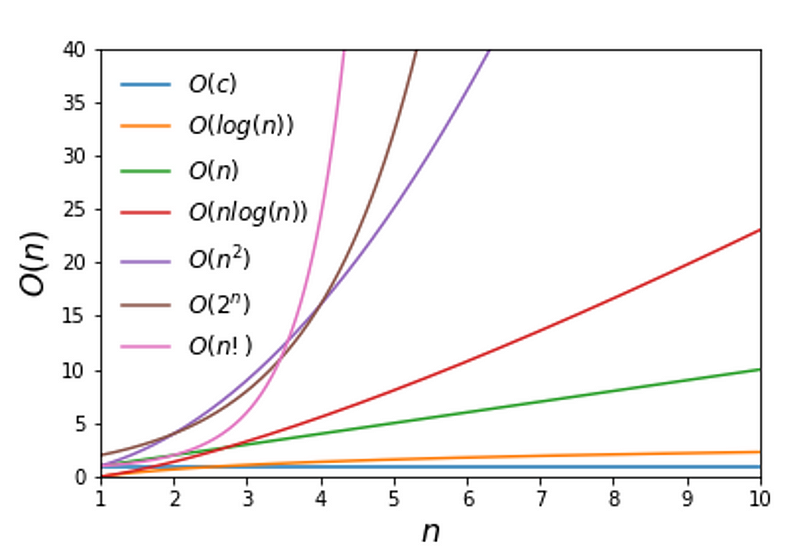
Figure 1: Graphical representation of different computational complexities
Now, let’s explore complexity in terms of time and space.
Section 1.1: Time Complexity
Time complexity, usually denoted as T(n), indicates how long it takes to perform a specific operation or series of operations based on the number of elements involved. To analyze time complexity, we start by examining the control structures within the code. For instance, an "if-else" structure has linear time complexity O(n), since each condition check accounts for one operation. Consider the following Python function:
def say(something):
if type(something) == str:
print(something)else:
print(str(something))
This function processes one input at a time and prints it after performing a type check. Running this function n times with different inputs results in a total time of O(n).
Another common scenario with linear time complexity involves loops. Most iterative algorithms with a single loop (as opposed to nested loops) will likely exhibit linear time complexity. This is because increasing the number of iterations by a factor of two will also double the time taken, assuming each iteration takes a relatively constant amount of time. However, when a loop is nested inside another, the complexity escalates to O(n²).
For example, if you have two for-loops operating over the same range of n iterations:
n = 10
for i in range(n):
for j in range(n):
<some operation>
In this case, the total number of iterations becomes n × n = n², resulting in a complexity of O(n²). While some may believe recursion is a more efficient approach, each recursive call consumes memory, leading to greater memory usage as the recursion depth increases. Thus, whenever feasible, iterative methods should be preferred over recursion.
Subsection 1.1.1: Space Complexity
Space complexity pertains to the memory (RAM) required to store data while an algorithm executes. An algorithm's space complexity increases with the amount of data it handles. Notably, space complexity does not always align with time complexity for the same algorithm; often, there is a trade-off: optimizing for lower space complexity can lead to higher time complexity, and vice versa.
Section 1.2: Summary of Complexity Types
While the discussion on computational complexity can be extensive, we will conclude with a summary table of common operations and their associated time complexities.

Table 1: Overview of common operations alongside their time complexities
Chapter 2: Further Exploration of Complexity
This video titled "Algorithms Explained: Computational Complexity" provides a detailed overview of computational complexity, breaking down its key concepts and significance in computer science.
In the video "What is Time Complexity Analysis? - Basics of Algorithms," viewers will learn the foundational principles of time complexity analysis, illustrated with real-world examples.