Exploring the Role of Geometry in Modern Physics
Written on
Chapter 1: The Geometry of Physics
In my contemporary physics classes, I grasped how vital shapes are in the realm of physics. Shapes form the foundation for fascinating physical phenomena, as they dictate the symmetry and dynamics of various systems. A shape is essentially any geometric entity, and in physics, we often deal with smooth forms.

Image by Free-Photos from Pixabay
This article will delve into the concept of manifolds. Manifolds are specific types of shapes frequently employed in physics due to their advantageous properties. They enable us to apply a coordinate system at any location, and they can also encapsulate vital information on their surfaces, which is key to comprehending the motion of objects.
Manifolds are prevalent across nearly all domains of modern physics. I studied them most rigorously in geometrically rich subjects such as general relativity, but they also frequently appear in particle physics.
However, let’s first examine the simplest shape: open space.
Section 1.1: Understanding Open Space
The physics concepts we encountered in high school likely revolved around the most fundamental shape—open space. Typically, when we refer to open space, we mean either a two-dimensional or three-dimensional expanse extending infinitely. In three dimensions, this resembles an astronaut floating in the void of space. This kind of open space is termed 'Euclidean space'. More specifically, mathematicians denote two-dimensional open space as R² and three-dimensional as R³, where R signifies 'real numbers' and the 2 or 3 indicates the number of dimensions required to pinpoint a location.
Euclidean space is significant because it allows mathematicians to easily construct a coordinate system that uniquely identifies any point within that space. For instance, if I provided you with a blank sheet of paper and we agreed on a common origin, I could indicate a specific location by giving you two coordinates. For example, I might say, "point out (1, 3)," and you would know exactly where to look.
The ability to establish coordinates in a space is crucial for spatial communication. For instance, consider a circle. Is it immediately clear that I can assign coordinates to locate a point on a circle? Perhaps not. It also raises the question of whether I can do the same for a sphere or a torus.
Section 1.2: What is a Manifold?
These considerations lead us to the definition of a manifold. A manifold is a geometric entity that locally resembles 'open space' across one, two, three, or any number of dimensions. The term "locally" refers to the vicinity surrounding any given point, in contrast to "globally," which describes the overall view of the shape. This distinction between local and global perspectives is crucial, and I will illustrate this with an example.
Consider a person standing on the surface of a sphere. Although the sphere does not resemble open space globally, when we zoom in on a specific point, the situation changes. In the immediate vicinity, it appears flat, leading one to initially believe the world is flat. Thus, locally, the area around any point on a sphere resembles R². Therefore, in three dimensions, a manifold M is a shape that appears as a 'flat plane' from the viewpoint of an observer on its surface.
At every 'neighborhood' on this manifold, a mapping exists that transforms the area around a point into open space. If the open space is of dimension n, this object is classified as an n-dimensional manifold. For instance, while a sphere is a three-dimensional object, the flat area at any point on its surface only resembles a two-dimensional plane. Thus, we classify the sphere as a two-dimensional manifold. Similarly, a circle is considered a one-dimensional manifold since any cross-section of the circle appears as a line.
Section 1.3: The Importance of Local Coordinates
If you've been following along and are puzzled about the significance of defining such an object, you're not alone. So why invest the effort in defining manifolds? The ability to map local areas to open space allows us to affix a coordinate system for orientation. For example, I can look around my office in London. If I wish to navigate to Hyde Park, I can consult a map with a coordinate system that facilitates my journey. This capacity to assign coordinates locally at any point on Earth is what qualifies a sphere as a manifold.
Not every shape qualifies as a manifold. For example, consider a cube. While the faces of the cube resemble R² locally, issues arise at its corners. At the corners, it is impossible to assign a coordinate system that maintains a flat appearance if one is positioned there.
In mathematics, significant study is dedicated to discerning when an object qualifies as a manifold. This understanding is vital for establishing when we can apply a coordinate system in physics. There are numerous proofs and embedding theorems in mathematics that determine the legitimacy of a curve in space as a manifold.
Chapter 2: Applications of Manifolds in Physics
The first video, "How geometry created modern physics – with Yang-Hui He," discusses the foundational role geometry plays in shaping modern physics, offering insights into how geometric concepts have influenced our understanding of the universe.
The second video, "Geometry for Physics," explores various geometric frameworks utilized in physics, demonstrating how these structures enhance our comprehension of physical phenomena.
What can we do with manifolds?
Having established a smooth coordinate system on a manifold at any point allows us to define mathematical entities such as curves and functions. For instance, a function on a manifold can be likened to a 'heatmap'—assigning a numerical value at any point. Thanks to the attached coordinate system, several fundamental mathematical concepts are now clearly defined. For example:
- We can assess whether functions on a manifold are smooth by checking their differentiability.
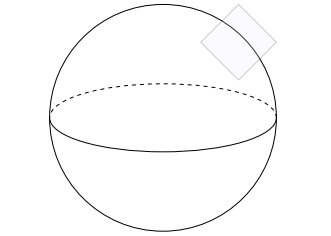
- We can also define 'tangent spaces'. In the sphere diagram previously mentioned, a tangent space is represented as a rectangle adjacent to the surface, illustrating the space experienced by an ant traversing the surface. Tangent spaces serve as foundational components in general relativity and modern classical mechanics, enabling us to understand how objects transition from one point in the manifold to another.
Additionally, certain symmetry structures in physics are manifolds themselves, known as Lie groups. The concept of a Lie group is fairly straightforward. Lie groups represent mathematical objects that describe smooth transformations. For example, the symmetry group governing the rotations of an object forms a Lie group since rotations are 'smooth' transformations. This smoothness implies that a slight rotation is possible. Conversely, transformations like reflections do not possess this property, as one cannot reflect an object by a minuscule amount.
The connection between Lie groups and manifolds is subtle. Consider the act of rotating an object: the degree of rotation specifies the transformation's parameters, confined between 0 and 360 degrees. This parameterization is also the precise information needed to identify a location on a circle, which itself is a manifold.
The association between symmetry groups and specific shapes renders Lie groups significant in examining symmetry structures in particle physics. Semi-simple Lie groups, in particular, are categorized into several distinct families. It turns out that all finite semi-simple Lie algebras can be organized into four infinite families denoted as An, Bn, Cn, Dn, along with five exceptional cases: E6, E7, E8, G2, and G4. This organizational system is referred to as the Cartan classification for Lie algebras.
Thus, a Lie group embodies a collection of continuous transformations that depend smoothly on n given parameters, making it an n-dimensional manifold.
Chapter 3: Classifying Manifolds
Mathematicians enjoy organizing and categorizing different mathematical objects, as classification aids in identifying genuinely distinct shapes or manifolds. We can classify manifolds based on their topological properties, which are inherent characteristics of a shape. The following points outline some key properties:
- Connectedness: This property indicates that we can draw a smooth path from any point in the manifold to any other. For instance, a sphere is connected, whereas a structure consisting of two spheres is not.
- Simply connectedness: This is a nuanced concept derived from homotopy groups. A space is considered 'simply connected' if any loop on its surface can be continuously transformed into a point. In contrast, a solid torus is not simply connected, as one can 'tie a string' around its center.
- Compactness: A space is compact if it can be covered by a finite number of subsets. In simple terms, this means that the object is not 'infinite', like open space. A sphere, for example, is compact, while an infinite line, which is a manifold, is not. This condition is equivalent to saying that if we embed the space in R³, the subset is closed and bounded. Thus, a quadratic curve on R is not a compact manifold as it is unbounded.
Conclusion
I hope this article serves as an insightful introduction to the concept of manifolds and their application in modern physics! Stay tuned for more discussions. If you're interested in further exploration, I host a physics blog where you can learn more!
References
[1] Introduction to Smooth Manifolds, John Lee, 2012 DOI: 10.1007/978–1–4419–9982–5